（これまでの増井俊之の「界面潮流」はこちら）

何かの練習を始めるとき、最初のうちは上達が実感できるものの、続けるうちに上達の速度が落ちたりスランプに悩んだりすることは誰もが経験することだと思います。

ワインバーグの名著「ライト、ついてますか」などの翻訳者としても有名な東京工業大学名誉教授の木村泉氏は、練習量と上達の関係を定量的に評価したいと考え、大量の折り紙を自分で折るのに要する時間を計ることによってその関係について考察しました。

木村氏は、吉澤章氏の「創作折り紙」という本で紹介されている「みそさざい」という作品を15万回折り続け、折るのにかかった時間がどのように変化したかを記録しました。折るのに要した時間を縦軸に/試行回数を横軸にして両対数グラフを描いた結果として以下の図が報告されています。

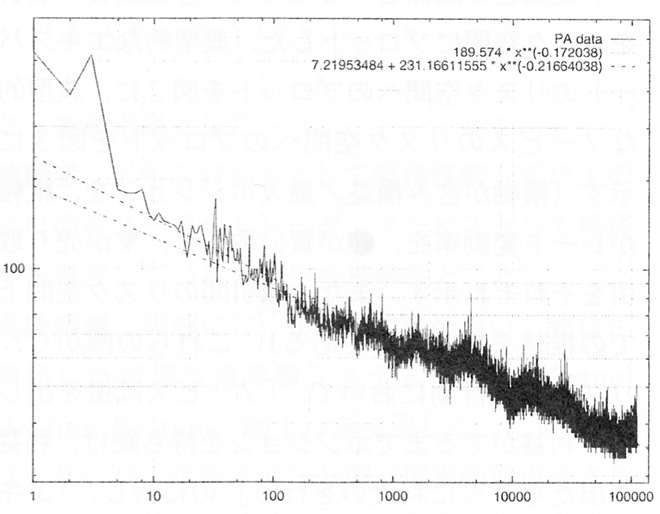
木村泉. 長期的技能習得データの「見晴らし台」とその意義. 日本認知科学会第20回大会発表論文集, pp.28-29, 2003.

同じ折り紙を15万回も折り続けて時間を計測するというのは尋常な努力ではありませんが、努力に見合った興味深い結果がこのグラフにあらわれています。このグラフでは以下のような特徴を見ることができます。

1. 練習回数と上達度は巾乗則に従う
   
   「なんでもフラクタル」の回で紹介しましたが、両対数グラフ上にプロットしたグラフが直線になるような関係があるとき、これらはべき乗則（冪乗測/巾乗則/Power Law）に従うといいます。実験結果を見ると上達度は奇麗に巾乗則に従っていることがわかります。このことを木村氏は練習の巾乗法則と名付け、様々な考察や実験を行なっています。
   
   たとえば2倍上達するのに100回の練習が必要なのであれば、2×2＝4倍上達するのに100×100=10000回の練習が必要だということになります。なかなか上達の道は厳しいことがわかります。
2. スランプの時期がある
   
   練習量と上達度はおよそ巾乗則に従うというものの、練習しても上達しない「スランプ」の時期が結構あることがわかります。スランプの時期は練習しても上達しないばかりか、かえって下手になっていくこともあります。スランプを脱出すると一気に上達が進み、大局的には巾乗則のとおり上達が進みます。
3. 値の揺れのパタンがある
   
   急速に上達したと思っても揺り戻しのようにスランプ状態になっている場合が何度も観測され、周期的にギザギザしたグラフになっています。揺れのパタンははっきりしませんが、フラクタル的な性質を持っている可能性があります。

上達の様子に何故このような傾向があるのかはさらなる研究が必要でしょうが、脳内でバックグラウンド的に試行錯誤が行なわれることによって、一時的には下手になったように見えつつも最終的に上達が目に見える形として出現しているように思われます。

計算機上での学習アルゴリズムでも同じようなパタンが見られることがあります。8×8のチェス盤と8個のクイーンを用意し、2個のクイーンが同じ行や列や斜め線上に並ばないように配置するという「8-Queen」というパズルがあります。計算機で8-Queenを解こうとする場合、端から順番に総当たりで解を捜すのが一般的ですが、確率的な最適化アルゴリズムである遺伝的アルゴリズムを使って解くこともできます。

下図は20×20の盤を使った「20-Queen」を遺伝的アルゴリズムで解いてみようとした例です。最初にランダムな解の集合を用意し、なるべくクイーンの衝突が少ないものが残るように遺伝的操作を繰り返しながら新しい世代を計算していくと、平均衝突数は下図のように減少していきます。

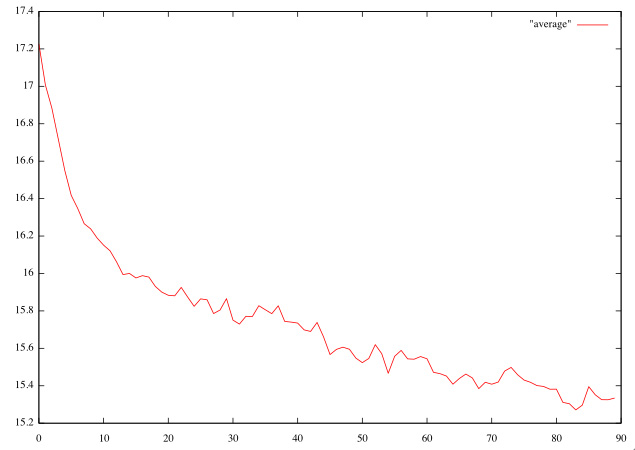
遺伝的アルゴリズムによる試行錯誤が行なわれた結果として解が最適値に近付いていく様子がわかりますが、単調に近付くのではなく、良くなったり悪くなったりしながら全体として最適解に近づいていく様子は折り紙の上達曲線と似ているといえるでしょう。

上達曲線の活用

人間の上達曲線にも計算機の学習曲線にもパタンが存在するのであれば、これをうまく活用する方法が考えられるでしょう。たとえば何かを練習しているとき、一度でもうまくいったことがあるならば、その後で多少スランプが続いたとしても「脳の中で試行錯誤が行なわれているのだ」と解釈して練習を続ければ、一定期間後にスランプを脱出できる可能性は高いでしょう。

木村氏のデータでは1万回目から2万回目までほとんど上達がみられていません。これだけスランプが続くと嫌になりそうなものですが、巾乗則を信じていたならば必ずスランプを乗り越えられると期待できたでしょうし、スランプ脱出の時期も大体予測できたから実験を続行できたのかもしれません。逆に、上達の見込みが無い場合はそのようなパタンが見られるでしょうから、早目に見切りをつける決心がつくかもしれません。

先が見えてしまうことは悲しいこともあるでしょうが、人生を無駄にしないためにこのようなデータを利用することは意義がありそうです。